LeetCode 97: Interleaving String

Problem Description

LeetCode Problem 97

Given strings s1, s2, and s3, find whether s3 is formed by an interleaving of s1 and s2.

An interleaving of two strings s and t is a configuration where s and t are divided into n and m substrings respectively, such that:

• s = s1 + s2 + … + sn
• t = t1 + t2 + … + tm
• |n - m| <= 1
• The interleaving is s1 + t1 + s2 + t2 + s3 + t3 + … or t1 + s1 + t2 + s2 + t3 + s3 + …

Note: a + b is the concatenation of strings a and b.

Example 1:

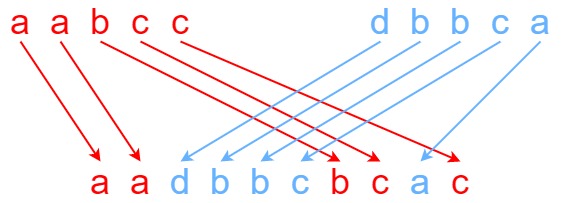
Input: s1 = “aabcc”, s2 = “dbbca”, s3 = “aadbbcbcac”
Output: true
Explanation: One way to obtain s3 is:
Split s1 into s1 = “aa” + “bc” + “c”, and s2 into s2 = “dbbc” + “a”.
Interleaving the two splits, we get “aa” + “dbbc” + “bc” + “a” + “c” = “aadbbcbcac”.
Since s3 can be obtained by interleaving s1 and s2, we return true.

Example 2:

Input: s1 = “aabcc”, s2 = “dbbca”, s3 = “aadbbbaccc”
Output: false
Explanation: Notice how it is impossible to interleave s2 with any other string to obtain s3.

Example 3:

Input: s1 = "", s2 = "", s3 = ""
Output: true

Constraints:

• 0 <= s1.length, s2.length <= 100
• 0 <= s3.length <= 200
• s1, s2, and s3 consist of lowercase English letters.

Follow up: Could you solve it using only O(s2.length) additional memory space?

Difficulty: Medium

Tags: string, dynamic programming

Rating: 94.33%

Solution Explanation

The solution uses dynamic programming to solve this problem efficiently. Let’s break down how it works:

Key Insights

1. For any position in s3, we need to determine if it can be formed by characters from s1 and s2 up to that point
2. We can build our solution incrementally by considering each character position and checking if we can use either s1 or s2’s next character
3. We use a 2D DP table where dp[i][j] represents whether we can form s3[0:i+j] using s1[0:i] and s2[0:j]

The DP Approach

The dp[i][j] entry will be true if either:

1. The current character in s1 (s1[i-1]) matches s3[i+j-1] AND dp[i-1][j] is true
2. The current character in s2 (s2[j-1]) matches s3[i+j-1] AND dp[i][j-1] is true

Base Cases

1. dp[0][0] = True (empty strings interleave to form empty string)
2. First row (i=0): Can we form using just s2?
3. First column (j=0): Can we form using just s1?

Visual Example

Let’s walk through Example 1 where:

• s1 = “aabcc”
• s2 = “dbbca”
• s3 = “aadbbcbcac”

Here’s how our DP table is filled (T = True, F = False):

     ''  d   b   b   c   a
''   T   F   F   F   F   F
a    T   F   F   F   F   F
a    T   T   T   T   T   T
b    F   T   T   F   F   F
c    F   F   T   T   T   F
c    F   F   F   T   T   T

Step-by-step for the first few cells:

1. dp[0][0] = True (empty strings match)
2. dp[1][0] = True (first ‘a’ from s1 matches s3)
3. dp[2][0] = True (second ‘a’ from s1 matches s3)
4. dp[0][1] = False (‘d’ from s2 doesn’t match first char of s3)
5. dp[1][1] = False (can’t match ‘ad’ with first char of s1)
6. dp[2][1] = True (can match “aad” using “aa” from s1 and “d” from s2)

Code

class Solution:
    def isInterleave(self, s1: str, s2: str, s3: str) -> bool:
        m, n = len(s1), len(s2)
        if m + n != len(s3): return False

        dp = [[False] * (n+1) for _ in range(m+1)]
        dp[0][0] = True

        # Initialize first row (using only s2)
        for j in range(1, n+1):
            dp[0][j] = dp[0][j-1] and s2[j-1] == s3[j-1]

        # Initialize first column (using only s1)
        for i in range(1, m+1):
            dp[i][0] = dp[i-1][0] and s1[i-1] == s3[i-1]

        for i in range(1, m+1):
            for j in range(1, n+1):
                c = s3[i+j-1]  # Current character in s3 we're trying to match

                # Try to match with s1's character
                if s1[i-1] == c:
                    dp[i][j] |= dp[i-1][j]

                # Try to match with s2's character
                if s2[j-1] == c:
                    dp[i][j] |= dp[i][j-1]

        return dp[m][n]

Space Optimization

To achieve $O(s2.length)$ space complexity as suggested in the follow-up question, we can optimize our solution to use a 1D array instead of a 2D table. This works because we only need the previous row’s information to compute the current row.

def isInterleave(self, s1: str, s2: str, s3: str) -> bool:
    m, n = len(s1), len(s2)
    if m + n != len(s3): 
        return False
        
    dp = [False] * (n + 1)
    dp[0] = True
    
    # Initialize first row
    for j in range(1, n + 1):
        dp[j] = dp[j-1] and s2[j-1] == s3[j-1]
    
    # Fill the table row by row
    for i in range(1, m + 1):
        dp[0] = dp[0] and s1[i-1] == s3[i-1]
        for j in range(1, n + 1):
            dp[j] = (dp[j] and s1[i-1] == s3[i+j-1]) or \
                    (dp[j-1] and s2[j-1] == s3[i+j-1])
    
    return dp[n]

Complexity Analysis

The solution has the following complexity characteristics:

• Time Complexity: $O(m \times n)$ where m and n are the lengths of s1 and s2 respectively
• Space Complexity:
  • Original solution: $O(m \times n)$
  • Optimized solution: $O(n)$

The optimized solution achieves the follow-up challenge of using only O(s2.length) additional memory space while maintaining the same time complexity.