LeetCode 807: Max Increase to Keep City Skyline

Problem Description

LeetCode Problem 807

There is a city composed of n x n blocks, where each block contains a single building shaped like a vertical square prism. You are given a 0-indexed n x n integer matrix grid where grid[r][c] represents the height of the building located in the block at row r and column c.

A city’s skyline is the outer contour formed by all the building when viewing the side of the city from a distance. The skyline from each cardinal direction north, east, south, and west may be different.

We are allowed to increase the height of any number of buildings by any amount (the amount can be different per building). The height of a 0-height building can also be increased. However, increasing the height of a building should not affect the city’s skyline from any cardinal direction.

Return the maximum total sum that the height of the buildings can be increased by without changing the city’s skyline from any cardinal direction.

Example 1:

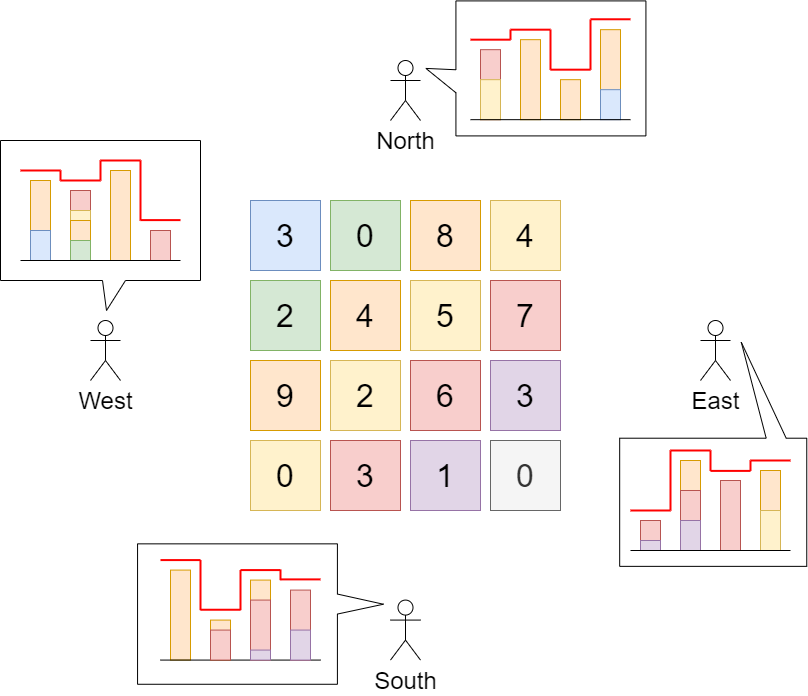
Input: grid = [[3,0,8,4],[2,4,5,7],[9,2,6,3],[0,3,1,0]]
Output: 35
Explanation: The building heights are shown in the center of the above image.
The skylines when viewed from each cardinal direction are drawn in red.
The grid after increasing the height of buildings without affecting skylines is:
gridNew = [ [8, 4, 8, 7],
[7, 4, 7, 7],
[9, 4, 8, 7],
[3, 3, 3, 3] ]

Example 2:

Input: grid = [[0,0,0],[0,0,0],[0,0,0]]
Output: 0
Explanation: Increasing the height of any building will result in the skyline changing.

Constraints:

• n == grid.length
• n == grid[r].length
• 2 <= n <= 50
• 0 <= grid[r][c] <= 100

Difficulty: Medium

Tags: array, greedy, matrix

Rating: 83.03%

Here’s my Python solution:

class Solution:
    def maxIncreaseKeepingSkyline(self, grid: List[List[int]]) -> int:
        n = len(grid)
        
        row_maxes = [max(row) for row in grid]
        
        # zip(*grid) transposes the matrix to easily get column maximums
        col_maxes = [max(col) for col in zip(*grid)]
        
        total_increase = 0
        
        for i in range(n):
            for j in range(n):
                new_height = min(row_maxes[i], col_maxes[j])
                total_increase += new_height - grid[i][j]
        
        return total_increase

Example Walkthrough

Let’s walk through Example 1 step by step:

Initial grid:

[3, 0, 8, 4]
[2, 4, 5, 7]
[9, 2, 6, 3]
[0, 3, 1, 0]

1. First, we calculate row_maxes:

   • Row 0: max([3, 0, 8, 4]) = 8
   • Row 1: max([2, 4, 5, 7]) = 7
   • Row 2: max([9, 2, 6, 3]) = 9
   • Row 3: max([0, 3, 1, 0]) = 3

   So, row_maxes = [8, 7, 9, 3]

2. Then, we calculate col_maxes:

   • Column 0: max([3, 2, 9, 0]) = 9
   • Column 1: max([0, 4, 2, 3]) = 4
   • Column 2: max([8, 5, 6, 1]) = 8
   • Column 3: max([4, 7, 3, 0]) = 7

   So, col_maxes = [9, 4, 8, 7]

3. For each position (i,j), we can increase the height to min(row_maxes[i], col_maxes[j]):

Final heights after increases:

[8, 4, 8, 7]  // Each value is min(row_max, col_max)
[7, 4, 7, 7]
[9, 4, 8, 7]
[3, 3, 3, 3]

Total increase = 35 (sum of all increases)

Complexity Analysis

• Time Complexity: $O(n²)$

  • Finding row and column maximums: $O(n²)$
  • Calculating total increase: $O(n²)$

• Space Complexity: $O(n)$

  • We store two arrays of length n for row and column maximums