LeetCode 516: Longest Palindromic Subsequence

Problem Description

LeetCode Problem 516

Given a string s, find the longest palindromic subsequence’s length in s.

A subsequence is a sequence that can be derived from another sequence by deleting some or no elements without changing the order of the remaining elements.

Example 1:

Input: s = “bbbab”
Output: 4
Explanation: One possible longest palindromic subsequence is “bbbb”.

Example 2:

Input: s = “cbbd”
Output: 2
Explanation: One possible longest palindromic subsequence is “bb”.

Constraints:

• 1 <= s.length <= 1000
• s consists only of lowercase English letters.

Difficulty: Medium

Tags: string, dynamic programming

Rating: 96.70%

Dynamic Programming Solution

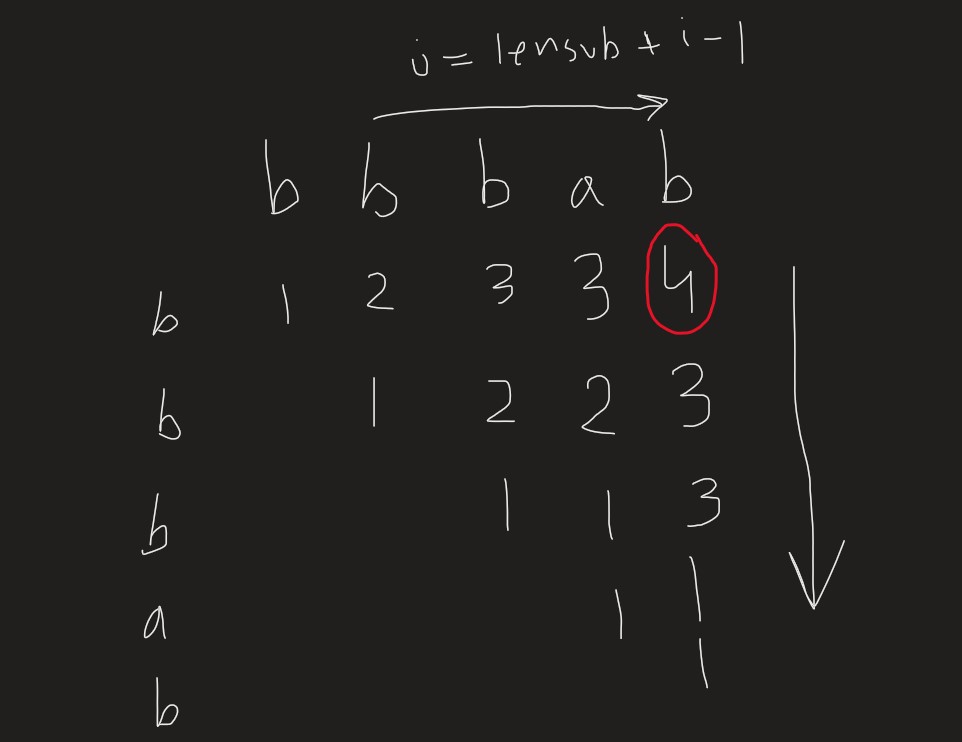
State Definition

Let’s define a 2D array dp where dp[i][j] represents the length of the longest palindromic subsequence in the substring s[i:j+1].

Base Cases

The base case is when the length of the substring is 1. In this case, the longest palindromic subsequence is 1.

for i in range(n):
    dp[i][i] = 1

Transition Function

If the characters at the start and end of the substring are the same, then the length of the longest palindromic subsequence is 2 plus the length of the longest palindromic subsequence in the substring s[i+1:j-1].

if s[i] == s[j]:
    dp[i][j] = 2 + dp[i+1][j-1]

If the characters at the start and end of the substring are different, then the length of the longest palindromic subsequence is the maximum of the length of the longest palindromic subsequence in the substring s[i+1:j] and the substring s[i:j-1].

else:
    dp[i][j] = max(dp[i+1][j], dp[i][j-1])

Solution

class Solution:
    def longestPalindromeSubseq(self, s: str) -> int:
        n = len(s)
        dp = [[0] * (n) for _ in range(n)]

        for i in range(n):
            dp[i][i] = 1

        for len_substr in range(2, n+1):
            for i in range(n-len_substr+1):
                j = i + len_substr - 1

                if s[i] == s[j]:
                    dp[i][j] = 2 + dp[i+1][j-1]
                else:
                    dp[i][j] = max(dp[i+1][j], dp[i][j-1])

        return dp[0][n-1]

Complexity Analysis

The solution has the following complexity characteristics:

• Time Complexity: $O(n²)$
• Space Complexity: $O(n)$

Note: This is an automated analysis and may not capture all edge cases or specific algorithmic optimizations.