LeetCode 2054: Two Best Non-Overlapping Events

Problem Description

LeetCode Problem 2054

You are given a 0-indexed 2D integer array of events where events[i] = [startTimei, endTimei, valuei]. The ith event starts at startTimei and ends at endTimei, and if you attend this event, you will receive a value of valuei. You can choose at most two non-overlapping events to attend such that the sum of their values is maximized.

Return this maximum sum.

Note that the start time and end time is inclusive: that is, you cannot attend two events where one of them starts and the other ends at the same time. More specifically, if you attend an event with end time t, the next event must start at or after t + 1.

Example 1:

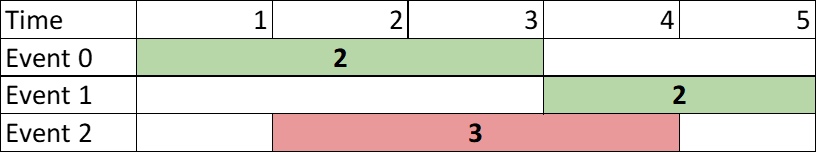
Input: events = [[1,3,2],[4,5,2],[2,4,3]]
Output: 4
Explanation: Choose the green events, 0 and 1 for a sum of 2 + 2 = 4.

Example 2:

Input: events = [[1,3,2],[4,5,2],[1,5,5]]
Output: 5
Explanation: Choose event 2 for a sum of 5.

Example 3:

Input: events = [[1,5,3],[1,5,1],[6,6,5]]
Output: 8
Explanation: Choose events 0 and 2 for a sum of 3 + 5 = 8.

Constraints:

• 2 <= events.length <= 105
• events[i].length == 3
• 1 <= startTimei <= endTimei <= 109
• 1 <= valuei <= 106

Difficulty: Medium

Tags: array, binary search, dynamic programming, sorting, heap (priority queue)

Rating: 96.28%

Intuition Behind the Solution

Before diving into the code, let’s understand the key insights that lead to an efficient solution:

1. Sorting by End Time: By sorting events by their end times, we ensure that when we process an event, we’ve already seen all events that could possibly come before it.

2. Dynamic Programming Array: We maintain an array that keeps track of the maximum value we can achieve ending at or before each event’s end time. This helps us quickly look up the best value we can get from events before any given start time.

3. Binary Search Optimization: Since our events are sorted by end time, we can use binary search to efficiently find the latest event that ends before our current event starts.

Solution with Detailed Walkthrough

class Solution:
    def maxTwoEvents(self, events: List[List[int]]) -> int:
        # Sort events by end time to process them in chronological order
        events.sort(key=lambda x: x[1])
        n = len(events)

        # dp[i] stores the maximum value achievable from events[0:i+1]
        dp = [0] * n
        dp[0] = events[0][2]  # Initialize with first event's value
        
        # Build dp array - at each point, take max of current event or best previous
        for i in range(1, n):
            dp[i] = max(dp[i-1], events[i][2])
        
        # Initialize result with best single event
        res = dp[-1]

        # Try each event as the second event
        for i in range(n):
            start, end, value = events[i]

            # Binary search for the rightmost event that ends before this one starts
            left, right = 0, i
            while left < right:
                mid = (left + right) // 2
                if events[mid][1] < start:
                    left = mid + 1
                else:
                    right = mid
            
            # If we found a valid previous event
            if left > 0:
                res = max(res, value + dp[left-1])
            
        return res

Example Walkthrough

Let’s walk through Example 1 where events = [[1,3,2], [4,5,2], [2,4,3]]:

1. Initial Sorting

   • First, we sort by end time:
   • [[1,3,2], [2,4,3], [4,5,2]]

2. Building the DP Array

   • dp[0] = 2 (value of first event)
   • dp[1] = max(2, 3) = 3 (max value seen up to second event)
   • dp[2] = max(3, 2) = 3 (max value seen up to third event)

3. Finding Best Two-Event Combinations

   • For each event as the second event:

   Event [1,3,2]:

   • No events end before time 1
   • Maximum = 2

   Event [2,4,3]:

   • Only [1,3,2] ends before start time 2
   • Value = 3 + 2 = 5

   Event [4,5,2]:

   • Both previous events end before time 4
   • Best previous value = 3
   • Value = 2 + 3 = 5

4. Final Result

   • The maximum value achievable is 4 by selecting events [1,3,2] and [4,5,2]

Complexity Analysis

The solution has the following complexity characteristics:

• Time Complexity: $O(n * log n)$
• Space Complexity: $O(n)$

Note: This is an automated analysis and may not capture all edge cases or specific algorithmic optimizations.