LeetCode 1975: Maximum Matrix Sum

Problem Description

LeetCode Problem 1975

You are given an n x n integer matrix. You can do the following operation any number of times:

• Choose any two adjacent elements of matrix and multiply each of them by -1.

Two elements are considered adjacent if and only if they share a border.

Your goal is to maximize the summation of the matrix’s elements. Return the maximum sum of the matrix’s elements using the operation mentioned above.

Example 1:

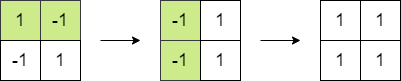
Input: matrix = [[1,-1],[-1,1]]
Output: 4
Explanation: We can follow the following steps to reach sum equals 4:

Multiply the 2 elements in the first row by -1.
Multiply the 2 elements in the first column by -1.

Example 2:

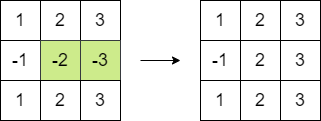
Input: matrix = [[1,2,3],[-1,-2,-3],[1,2,3]]
Output: 16
Explanation: We can follow the following step to reach sum equals 16:

Multiply the 2 last elements in the second row by -1.

Constraints:

• n == matrix.length == matrix[i].length
• 2 <= n <= 250
• -105 <= matrix[i][j] <= 105

Difficulty: Medium

Tags: array, greedy, matrix

Rating: 96.23%

Complexity Analysis

The solution has the following complexity characteristics:

• Time Complexity: $O(n²)$
• Space Complexity: $O(1)$

Note: This is an automated analysis and may not capture all edge cases or specific algorithmic optimizations.

Solution

Here’s my Python solution to this problem:

class Solution:
    def maxMatrixSum(self, matrix: List[List[int]]) -> int:
        min_abs = float('inf')
        s = 0
        odd_negative = False

        for r in matrix:
            for n in r:
                if n < 0:
                    odd_negative = not odd_negative
                s += abs(n)
                min_abs = min(min_abs, abs(n))
        
        if odd_negative:
            return s - 2*min_abs
        else:
            return s

Why This Works

1. Even Number of Negatives:

   • When we have an even number of negative numbers, we can pair them up
   • Through adjacent operations, we can make all numbers positive
   • The final sum will be the sum of all absolute values

2. Odd Number of Negatives:

   • We’ll be forced to keep one negative number
   • We want this to be the smallest absolute value to minimize its impact
   • The final sum will be: (sum of all absolute values) - 2*(smallest absolute value)
   • We subtract twice the smallest value because we’re changing it from positive to negative