LeetCode 115: Distinct Subsequences

Problem Description

LeetCode Problem 115

Given two strings s and t, return the number of distinct subsequences of s which equals t.

The test cases are generated so that the answer fits on a 32-bit signed integer.

Example 1:

Input: s = “rabbbit”, t = “rabbit”
Output: 3
Explanation:
As shown below, there are 3 ways you can generate “rabbit” from s.
rabbbit
rabbbit
rabbbit

Example 2:

Input: s = “babgbag”, t = “bag”
Output: 5
Explanation:
As shown below, there are 5 ways you can generate “bag” from s.
babgbag
babgbag
babgbag
babgbag
babgbag

Constraints:

• 1 <= s.length, t.length <= 1000
• s and t consist of English letters.

Difficulty: Hard

Tags: string, dynamic programming

Rating: 95.75%

Dynamic Programming Solution

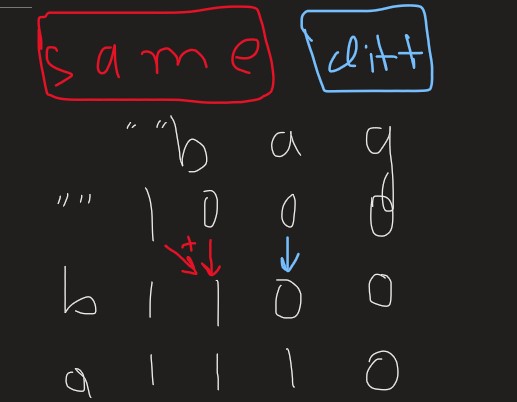
State Definition

Let dp[i][j] represent the number of distinct subsequences of s[0…i-1] that equal t[0…j-1].

Base Cases

1. Empty string t is a subsequence of any string exactly once:
   • dp[i][0] = 1 for all i
2. Empty string s has no subsequences equal to non-empty t:
   • dp[0][j] = 0 for all j > 0

Recurrence Relation

For each position i in s and j in t, we have two cases:

1. If s[i-1] == t[j-1]:

   • We can either use the current character: dp[i-1][j-1]
   • Or skip it: dp[i-1][j]
   • Therefore: dp[i][j] = dp[i-1][j-1] + dp[i-1][j]

2. If s[i-1] != t[j-1]:

   • We must skip the current character
   • Therefore: dp[i][j] = dp[i-1][j]

Solution

Here’s my Python solution to this problem:

class Solution:
    def numDistinct(self, s: str, t: str) -> int:
        m, n = len(s), len(t)

        dp = [[0] * (n+1) for _ in range(m+1)]

        #Empty string t is a subsequence of any string exactly once
        for i in range(m+1):
            dp[i][0] = 1


        for i in range(1, m+1):
            for j in range(1, n+1):
                if s[i-1] == t[j-1]:
                    dp[i][j] = dp[i-1][j-1] + dp[i-1][j]
                else:
                    dp[i][j] = dp[i-1][j]
        
        return dp[m][n]

Complexity Analysis

The solution has the following complexity characteristics:

Time Complexity: $O(m×n)$

• We fill a table of size m×n
• Each cell requires O(1) computation

Space Complexity: $O(m×n)$

• We need a 2D table to store intermediate results
• Can be optimized to O(n) using rolling arrays